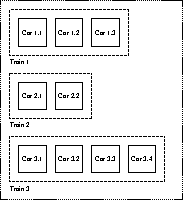
Figure 1: Mature object space structure
Jacob Seligmann & Steffen Grarup
Computer Science Department, Aarhus University
Ny Munkegade 116, DK-8000 Århus C, Denmark
E-mail: {jacobse,grarup}@cs.au.dk
Recently, Hudson & Moss have introduced an exciting new algorithm, the Train Algorithm, for performing efficient incremental collection of old generation space [HM92]. Using the algorithm, generational collectors can be extended to provide non-disruptive collection of all generational areas.
In the following, we present the results from a practical implementation of the Train Algorithm [GS93]. Section 2 describes the basic ideas behind the algorithm. Section 3 concerns the practical implementation issues. Section 4 presents the measurement results. Section 5 points out future research directions.
Section 2.1 outlines the main ideas behind the algorithm and introduces the terminology needed in later sections. (Readers familiar with the algorithm may wish to skip this part.) Section 2.2 identifies and corrects a subtle error in the original algorithm. Section 2.3 addresses the treatment of highly referenced objects.
To achieve this, the algorithm arranges the blocks into disjoint sets. With a striking metaphor, Hudson & Moss refer to the blocks as cars, and to the set of blocks to which a car belongs as its train. Mature object space can then be thought of as a giant railway station with trains lined up on its tracks, as illustrated in Figure 1.

Figure 1: Mature object space structure
Just as in real life, cars belong to exactly one train and are ordered within that train. The trains, in turn, are ordered by giving them sequence numbers as they are created. This imposes a global lexicographical ordering on the blocks in mature object space: One block precedes another if it resides in a lower numbered (i.e. older) train; or if both blocks belong to the same train, then if that block has a lower car number (i.e. was added to the train earlier on) than the other. In the example structure shown in Figure 1, Car 1.1 precedes Car 1.2, Car 1.2 precedes Car 1.3, Car 1.3 precedes Car 2.1, and so on.
Intuitively, the Train Algorithm works by constantly clustering sets of related objects. In this way, it eventually collapses any interlinked garbage structure into the same train, no matter how complex. In the following, we shall see how this is achieved.
First, a check is made to see whether there are any references into the train to which the car being collected belongs. If this is not the case, then the entire train contains only garbage and all its cars are reclaimed immediately. (This is the part of the algorithm which enables large cyclic garbage structures to be recognized and reclaimed, even if they are too big to fit into a single car. Section 2.2 explains why such structures always end up in the same train.)
Otherwise, all objects residing in the car being collected referenced from outside the train are evacuated as follows. Objects referenced from other trains are moved to those trains; objects referenced from outside mature object space are moved to any train except the one being collected. If a receiving train runs full, a new car is simply created and hooked onto its end. Then, in typical copy collector style, evacuated objects are scanned for pointers into the car being collected, moving the objects thus found into the train from which they are now referenced, and so on.
With the transitive closure of all externally referenced objects having been evacuated, the only live objects in the car being processed are those referenced (exclusively) from cars further down the train being collected. Such objects are evacuated to the last car of the train, as are the objects they reference, etc.
At this point, none of the objects remaining in the car being collected are referenced from the outside and are therefore garbage. Thus, the space occupied by the car is reclaimed and the collection is finished.
The remembered sets are maintained by extending the generational pointer assignment run-time check (the write barrier). In addition to the traditional recording of references from older to younger generations, all pointer assignments between mature objects must now also be examined and possibly recorded in an old car remembered set. By letting the size of the old generation cars be of the form 2^n bytes, allocated on a 2^n byte boundary, one can maintain a train table over the train and car number associated with each mature object space block. Given a pointer address, the train table information can be quickly accessed by right-shifting the address n bits and using the result as an index [HMDW91].
This argument, of course, requires that all trains are eventually processed. Unfortunately, the Train Algorithm as presented so far provides no such guarantee. Consider the situation shown in Figure 2. A-B is a live structure, with object B referenced from some root. For the sake of simplicity, objects A and B are assumed to be too big to fit into the same car (more realistically, they could be large interlinked structures). When the car containing A is collected, A is simply moved into a new car at the end of the train. We call such collections futile because they neither evacuate, nor reclaim, objects. Now, before the next invocation of the algorithm (in which we would have hoped to evacuate object B), the mutator may change the root reference to point to A instead of B. Thus, at the beginning of the next collection, the overall object structure may be entirely unchanged. If the mutator continues to swap references behind the collector's back, it will force the collector to keep processing the A-B structure, thus never getting around to any of the other trains in the system.
This situation may be prevented as follows. Whenever a futile collection occurs, one of the external references to objects further down the train are recorded. (Such a reference must exist, otherwise the entire train would have been reclaimed.) A reference thus recorded is then used as an additional root for subsequent collections and is not discarded until a non-futile collection occurs. In the example above, this would cause the root reference to be recorded after the first collection, causing object B to be evacuated from the train at the next invocation of the algorithm even though it is no longer directly referenced.
Using this extension, it can be shown that each pass over a train will either reclaim or evacuate at least one object, and the entire Train Algorithm may be proven formally correct [GS93].
As an alternative approach, Hudson & Moss tentatively suggest that cars containing popular objects should not be collected at all. Instead, such cars should be retained, logically (but not physically) moving them to the end of the newest train [HM92, Section 6]. Unfortunately, a closer analysis shows that this approach may leave garbage undetected, so a number of refinements are needed.
First, one cannot simply retain popular cars, but must evacuate all non-popular objects from them. Otherwise, garbage contained in or referenced from popular cars will not be detected and reclaimed.
Second, one should not move popular cars to the end of the newest train. This would cause large garbage structures scattered across several trains each containing a popular member to survive forever because such structures would never be collapsed. Instead, popular cars should only be moved to the end of the highest numbered train from which they are referenced.
Third, cars containing several unrelated popular objects pose a problem. Such cars will have to be split in some way so that each popular object can be moved to the end of the highest numbered train from which it is referenced.
With the popular object treatment outlined above, the Train Algorithm can be shown to correctly identify and reclaim all garbage [GS93]. However, such schemes may be quite costly to implement in practice. Since the remembered sets associated with popular cars may be arbitrarily large, one cannot afford to run through them to find references to non-popular objects, or to find the highest numbered train from which a popular object is referenced. Also, logically split cars are not easily handled in a train table setting. A naive way to overcome these problems would be to associate a remembered set with each object, to always maintain the highest numbered train from which an object is referenced, and to extend the train table with balanced binary search trees for split areas. In practice, more sophisticated solutions are undoubtedly needed to make the popular car approach a viable alternative to pointer indirection.
This section describes the implementation process. Section 3.1 presents the memory layout used in the two systems. Section 3.2 concerns the practical issues that had to be addressed. Section 3.3 discusses the overall implementation efforts.
The advancement age between the two generations is determined adaptively using demographic feedback-mediated tenuring [UJ92]. To record references from old to young objects, a hash table-based remembered set is maintained, using a traditional but quite efficient write barrier to examine pointer assignments at run-time.
The global remembered set (recording references from the entire old generation to the young one) was replaced by a remembered set for each car (recording references from that car to the young generation). This approach enabled us to immediately discard the relevant entries when a car was reclaimed, rather than run through a global table to purge out expired references.
Where should objects be moved when they are promoted? As objects were tenured into mature object space, we moved them into the last car of the newest train until the total size of the objects residing there exceeded a certain threshold (the fill limit) in which case we chose to create a new train. In this way, we tried to achieve a balance between initially having only a few objects in each train (to avoid accidental object structure infiltration which would require extra passes to disentangle) and putting many objects into each train (to avoid the storage overhead of having many sparsely filled cars in the system). We chose a default fill limit of 90%. The implications of this choice are presented in Section 4.5.
Our approach to finding the right balance was to select a fixed acceptable garbage percentage specifying the desired trade-off between speed and storage. Whenever the amount of garbage detected in mature object space was larger than expected, the collection frequency was automatically increased in order to keep memory consumption down; and whenever the garbage ratio was lower than expected, the collection frequency was decreased to improve the overall performance. In addition, we introduced an upper limit on the number of young generation collections between each old generation collection step. Without such a limit, the algorithm would be called much to seldomly if little or no garbage was detected for a while.
Technically, there were a few obstacles to calculating the garbage ratio. Whereas batch algorithms can compare the size of mature object space before and after a collection, this is not possible in the Train Algorithm setting, where only a small area is collected at each invocation, where some objects may be scanned more frequently than others, and where there are always parts of memory that have not yet been processed. By associating with each train a counter holding the amount of objects tenured directly into it, one can, however, calculate the desired figure. The result is somewhat delayed because it is first obtained when the newest train in the system at counter initialization time is reclaimed, that is, after an entire sweep over mature object space. By initializing a new counter each time the collection of a new train commences, estimates nevertheless become available quite often. This approach turned out to work well in practice [GS93].
Section 4.1 describes the benchmark system. Section 4.2 presents the most important result of our implementation, namely that disruptive old generation collection pauses can be completely removed using the Train Algorithm. Sections 4.3, 4.4, and 4.5 show the reverse side of the coin, namely the time, storage, and copying overheads induced. Section 4.6 concerns the special treatment of popular objects. Section 4.7 looks at the virtual memory behavior of the algorithm.
To ensure a wider exposure, we also measured the performance of an interactive run with the Sif hyper-structure editor [MIA90] and a discrete event simulation system modeling a series of orders pipelining through a set of machine queues.
Except for the benchmark described in Section 4.7, all measurements were carried out on a 40 MHz Sun SPARC IPX 4/50 workstation equipped with 32M bytes of primary memory. Apart from a few page faults at the beginning of each run, there was practically no virtual memory activity. The times reported in the following are therefore the sum of the user and system CPU times. In practice, this turned out to correspond quite closely to elapsed wall-clock time.
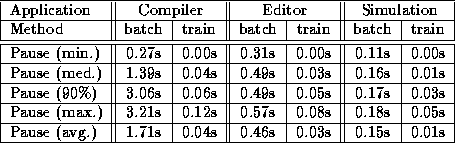
Table 1: Old generation collection pause distribution
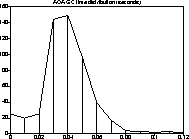
Figure 3: Pause distribution, compiler run
As can be seen, the new collector turned out to be extremely effective. For all three benchmark programs, it replaced a number of highly disruptive old generation collections with a series of non-disruptive ones, each just a few dozen milliseconds long. Thus, the Train Algorithm lived up to its promises of delivering pause times suitable for use in interactive systems.

Table 2: Total time distribution
Table 2 shows the total time spent in the various system components. In addition, approximately one second was spent on large object area free-list compaction in the compiler and editor runs. Since the Train Algorithm did not influence large object area management in any significant way, we shall not go further into that issue here.
In any case, the differences in old generation collection times were practically negligible in the overall picture. The extra time spent in the compiler and simulation runs corresponded to merely 0.4% of the total execution time of the programs, and the time (seemingly) saved in the editor session amounted to only 0.2%.
For the compiler and editor runs, this amounted to an increase of about 0.0025 seconds for each young generation scavenge, or between 7% and 8%. For the simulation run, the result was a decrease in young generation collection time of about 25%. In all three cases, we believe that the main reason for the difference was the time spent scanning the remembered sets for roots. In the compiler and editor runs, the accumulated size of the remembered sets associated with the old generation cars far exceeded that of the single remembered set originally employed; in the simulation run, the accumulated size was significantly smaller.
Overall, the differences in young generation collection times corresponded to an increase in execution time of about 1% for the compiler and editor runs, and a decrease of almost 5% for the simulation session.
For the compiler run, the net result was a 0.9% decrease in mutator time. For the editor session, a 0.5% increase was observed, while the total simulation mutator time decreased by 4%. In the overall picture the differences were, of course, slightly less.
Even though BETA objects are generally highly interlinked because they all contain an environment reference (the origin) to their statically enclosing object, this was a surprisingly large figure. However, by fine-tuning the hash function and rehash strategies, we believe that the overhead could be significantly reduced.
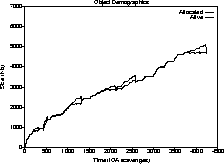
Figure 4: Mark-sweep garbage overhead
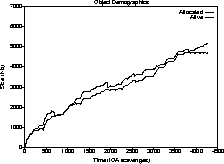
Figure 5: Train Algorithm garbage overhead
In the original system, new mature object space blocks were only allocated if the total old generation capacity was very close to being exhausted after a mark-sweep collection. Therefore, the difference between the two graphs was always less than the size of an old generation block, 512K bytes, as seen in Figure 4. In the Train Algorithm-based system, we chose to aim for a 10% garbage ratio and were quite successful, as seen in Figure 5.
Thus, the storage overhead caused by unprocessed garbage was about 10% for the compiler run. The same behavior was achieved for the editor session, while the old generation storage requirements fell a bit for the simulation run, simply because the program needed less old generation space than the size of the single block allocated in the mark-sweep implementation, and because the Train Algorithm collector managed to keep up with the high mortality rate.
Had we had more control over which parts of memory were used for heap allocation, we could have allocated a smaller train table. For instance, had it been known that only the lowest 256M bytes of memory would ever be used, a 16K bytes table with 4K entries would have sufficed. However, this may not have been worth the effort since any unused parts of the train table would be swapped out by the virtual memory system as needed.
In order to get an impression of the Train Algorithm's practical behavior in this area, we recorded information about the number of cars in each train and the number of collections it took to reclaim one using various fill limits (see Section 3.2.1). As it turned out, the compiler benchmark gave rise to the most complex object structures. The results of this run are shown in Table 3.
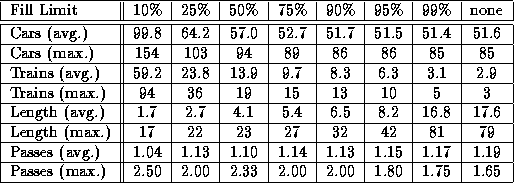
Table 3: Train structure statistics
The first six rows show the average and maximum number of cars and trains in the system, as well as the train length. The last two rows show the number of passes needed to reclaim each train, expressed as the ratio between the number of invocations performed and the initial length of the train. Thus, a lower ratio signifies less superfluous copying.
As should be expected, lowering the fill limit resulted in more, shorter trains which required fewer passes to be reclaimed. The cost for this behavior was an increase in the number of cars, and thus in the overall storage consumption. However, even in the most storage preserving setting in which new trains were only created when the collection process reached the newest train and needed somewhere else to evacuate objects to, the average amount of redundant copying was less than 20%. Thus, we did not see any signs of worst-case behavior occurring in practice.
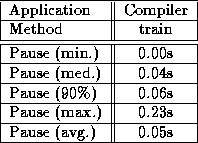
Table 4: No popular treatment, pause table
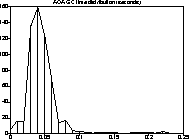
Figure 6: No popular treatment, pause plot
As can be seen, the maximum collection time doubled. This was because there were more than 50,000 references to the basic environment object, causing over 200K bytes of pointers scattered throughout mature object space to be updated whenever the car containing it was collected. In addition, the total time spent on old generation collection rose to 26.56 seconds, or nearly 30%. This was because hundreds of inter-car remembered set insertions were now typically required at each collection step as objects referencing the basic environment object were evacuated past it.
As can be seen from the figures above, our simple popular object scheme therefore turned out to be highly effective in practice.
The mark-sweep and Train Algorithm collectors scanned roughly the same amount of mature object space during the execution, about 30M bytes. This gave rise to 3,800 page faults in the mark-sweep implementation, and 4,500 in the Train Algorithm implementation. In both cases, this corresponded to around 95% of the total number of page faults. While there were nearly 20% more page faults in the Train Algorithm implementation, they were far better temporally distributed. For instance, the last mark-sweep collection caused over 1,000 pages to be swapped into primary memory, spending 6.4 seconds in the system kernel alone (not counting the disk access). In contrast, the Train Algorithm collector caused an average of less than 10 page faults per collection step. Still, a few collections of cars with large remembered sets caused nearly 100 page faults each, with up to 0.25 seconds spent in the system kernel.
To gain a better impression of the virtual memory behavior of the Train Algorithm, more detailed measurements are required. Nevertheless, our simple experiment seems to indicate that the algorithm is certainly a step in the right direction.
____
_||__| | ______ ______ ______
( | | | | | | |
/-()---() ~ ()--() ~ ()--() ~ ()--()