Jørgen Lindskov Knudsen, Jens Middelfart
Computer Science Department, Aarhus University,
Ny Munkegade 116, DK-8000 Århus C, Denmark
E-mail: {jlknudsen,donjens}@cs.au.dk
Phone: (+45) 89 42 31 88 -- Fax: (+45) 89 42 32 55
Programming languages usually offers language constructs that primarily supports one of the above paradigms (such as Smalltalk supporting object-oriented programming and Miranda, supporting functional programming). A few languages are designed to support several paradigms (such as Leda, supporting procedural, functional, object-oriented, and logic programming.
Supporting several paradigms within one language is a very complex issue, primarily due to the nearly incompatible demands of the different paradigms (e.g. procedural programming is concerned with manipulating state, whereas functional programming totally abandons the notion of state).
However, the different paradigms offers elegant means for specifying solutions to a particular class of problems, which formulated by the means of one of the other paradigms results in far less elegant.
In this paper, we will present our work on supporting constraint programming within an inherently object-oriented language, namely BETA [BETA]. Our work is based on the assumption that it should be possible to apply the means from constraint programming within an otherwise object-oriented paradigm.
Due to the complex nature of extending a given language, and in order to minimize the problems of 'pay-for-non-use' (i.e. that programs have to pay some overhead (time or space), even when they are not using the means for constraint programming), we have chosen to design the support for constraints in BETA as a framework; that is, as a set of classes with the intended semantics. Programmers who intend to apply constraint programming in their solutions therefore uses these classes as the means for specifying the constraints, and it is then the responsibility of the constraint framework to ensure that the semantics of these constraints are upheld at any time (according to their specification).
Supporting constraint programming by means of a framework also offers very important means for creating specialized frameworks that are targeted towards specific constraint systems (e.g. constraint systems targeted towards graphical layout). Using frameworks for these specialized frameworks is then no different that using the original framework, except that the constraints are defined at a higher abstraction level, closer to the problem domain at hand (e.g. graphical layout).
The difference between constraint programming and e.g. procedural programming can best be described by the "Hello World" example within constraint programming: the Fahrenheit-Celsius conversion.
In both paradigms, we are having two variables, C and F, where C is the current temperature in Celsius and F is the current temperature in Fahrenheit. The problem is to ensure that C and F at any time holds the same temperature (in their respective scales).
The relation between the Fahrenheit and Celsius scales are defined by the following equation:
Celcius = (Fahrenheit - 32)*5/9
In procedural programming, the solution is to ensure, that both variables are updated, if one of them changes value:
F := newVal; C := (newVal - 32)*5/9
and
C := newVal; F := 32 + newVal*9/5
However, this process is very error-prune since it is fairly easy to forget the conversion somewhere in the program, and especially dangerous is later changes to the program, where the programmer might have forgotten about the demands for C and F to refer to the same temperature.
More importantly, in the case of large systems, the number of such conversions etc. might be very big and therefore difficult to maintain, and in the case of modifying new conversions to the system, it is very difficult to track all places in the system where these variables are changed, and then add the additional conversion code.
The solution within constraint programming is to consider the conversion not as a conversion, but as a constraint imposed on the two variables; a constraint which must be automatically maintained by underlying system when either of the variables are changed. E.g.:
constraint: C = (F -32)*5/9
It is now the responsibility of the runtime system to ensure, that if e.g. C changes value somewhere in the system:
C := newVal;
then the value of F is automatically changed immediately such that the constraint is maintained.
Using constraints, it is ensured that the constraint is maintained globally in the application, avoiding the problems of missing conversions etc., and avoiding that later changes to the program by mistake violates the constraint.
This description of constraints is (naturally) too simplified. In real-life constraint systems, a given variable may be controlled by many constraints, and a constraint may control more than two variables.
Constraints in a given system may give rise to problems, such as under-constrained systems, over-constrained systems, and ambiguous constraints.
An under-constrained system is a system where the constraints are not sufficient to define a unique set of values for the other variables, constrained by a given constraint, e.g.:
constraint: X < Y
is under-constrained (assuming no other constraints on X and Y), since if Y = 10, then setting X to e.g. 100 will imply that all values >100 are valid values for Y.
An over-constrained system is a system where the constraints are so strong, that no valid solutions can be found, e.g.:
constraint: X < Y
constraint: Y < 100
is over-constrained, since no solutions exists for e.g. X := 100.
These problems have resulted in the formulation of constraint hierarchies. A hierarchical constraint system is a system in which the constraints are given priorities and it is then the responsibility of the constraint system to find the best possible solution, possibly ignoring constraints with low priority. Actually, it is the responsibility of the constraint solver to find the constraints to be satisfied, and the responsibility of the constraint specifier (usually the programmer) to specify the best possible satisfaction, given the constraints, selected by the constraint solver.
Constraint hierarchies are especially useful for handling over-constrained systems, since the constraint system has the possibility to find a solution by ignoring some of the lower prioritized constraints and thus avoid to be forced to signal an error, which in many systems would be more or less disastrous.
We will in the rest of the paper only discuss constraint systems supporting constrains hierarchies.
Intuitively these systems seems to deal with the same type of properties: means for ensuring that a given application at any time is consistent in the sense that the state of the application always is ensured to be within some defined borders.
In an invariant system, invariants are defined on the state of variables, on the state of objects, or as pre- and postconditions to operations. Invariants are checked by the underlying system, just as constraints.
The difference between an invariant system and a constraint system arises when an invariant (or a constraint) is violated. In the constraint system (as described above), the underlying system takes action on this violation, and examines the state of the application to determine if changes can be made to this state to bring it back within the domain, defined by the constraints. If such a possibility exists, the constraint system (on its own initiative) changes the state of some (possibly other) variables to bring the application back within the domain of the constraints (possibly revoking some weaker constraints in the case of a constraint hierarchy).
In the invariant system, violations of the invariants are treated as severe runtime errors, and usually results in the invocation of some exception handling mechanism. It is then up to the application programmer to react to the exception, and possibly try to repair the invariant violation (or give up and terminate the application). An excellent example of an object-oriented invariant system can be found in the Eiffel Language definition. The Mjølner BETA System contains an experimental invariant system in the form of an invariant framework (along the same lines as the constraint framework described in this paper).
This implies that the concept of variables is somewhat different in object-oriented systems, namely variables as defining attributes of objects, containing the current state of the object. Variables in object-oriented systems are also often more complex since they are either containing entire objects (part-objects) or references to other objects. Naturally, variables in the traditional sense are still present in most object-oriented languages, but they play a far less important role, primarily as implementation means for the basics of objects.
In relation to constraint systems, this implies that we have to rethink the role of constraints, especially in relation to objects. Traditional variables does not pose any new considerations, and are therefore ignored in the following.
Constraints (in the traditional sense) are based on variables and the values of variables. But what is the value of an object variable (a variable containing a part object or an object reference). In essence that's the same as asking what is the value of an object?
There is no clear and general answer to this question, independent of the language, so we will here restrict ourselves to BETA. In general, measurements can be conducted on objects in BETA, and the result of such a measurement is represented by a (possibly composite) value. Such measurements are represented in the BETA language by the exit-part of the object descriptor. That is, one possible value of an object is the values that are the result of a measurement on an object. Another interesting (and important) value associated with an object, is the object identity (represented in BETA by object references).
This implies that the constraint system for object-oriented systems (at least in the case of BETA) will have to be able to deal with these two facets of object values, as well as being able to deal with whole-part constraints.
In theory, these measurements need to be side-effects-free in order to ensure that the constraint solver will be working properly, and without influencing the workings of the application (besides naturally constantly keeping the specified constraints satisfied).
The most common usage of whole-part constraints is to implement whole constraints in terms of constraints on the parts. This type on whole-part constraints ensures, that irrespectively of whether it is the state of the objects as a whole that is changed, or it is the state of some parts that have been changed, then the constraint solver will enforce the constraints to satisfy all constraints on the object (internal and external constraints).
As a minor issue, the constraint system must also be sufficiently flexible to allow constraints to be specified for parts of an object without necessary imposing a constraint on the objects as a whole. The following example illustrates these two aspects of whole-part constraints:[3]
(# point:
(# h,v: @Integer;
enter (h,v)
exit (h,v)
#);
equal: constraint(# ... #);
vertical: constraint
(# p1,p2: ^Point;
enter (p1[],p2[])
do (p1.h[],p2.h[])->equal;
#);
horizontal: constraint(# ... #);
p,q,r: @point;
do (p[],q[])->horizontal;
(p[],r[])->vertical;
(r.h,7)->equal;
#)In
this example, point is defined as a usual BETA pattern (class) with two
attributes, h and v, containing the coordinates of a point object. Equal is a
definition of a constraint, which ensures that two integers contain the same
value. The implementation of the equal constraint is not shown (to reduce the
size of this example).Vertical is a definition of another constraint. In this case, it is a constraint on point objects, and in the implementation it can be seen, that this constraint is expressed in terms of constraints on the parts of the two objects, namely by imposing the equal constraint on the h attribute of the two points. The horizontal constraint is defined similarly.
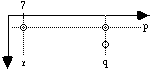
The example then defines three points, p, q, and r, and imposes the horizontal constraint between p and q, and the vertical constraints between p and r. Finally, r is constrained in its horizontal position to 7.
In graphical terms, this can be illustrated by (the dotted lines signify the
valid positions for the point):

Changing the BETA language was quickly abandoned (for the obvious reasons), and we began looking for ways to supply a framework for creating constraint systems. The first important decision would be to chose the appropriate constraint solver. We considered implementing (and in fact implemented) a local propagation constraint solver, but local propagation is a every limited mechanism for solving constraints; e.g. inability to cope with constraint hierarchies. We therefore looked for other constraint solvers, and found the so-called SkyBlue algorithm [SkyBlue].
SkyBlue is an efficient incremental constraint solving algorithm that is able to offer solutions to constraint hierarchies. SkyBlue uses local propagation to maintain sets of required and preferential constraints. SkyBlue is better than most other constraint solvers in that it allows cycles of constraints (even though it does not try to satisfy them), and it supports multi-output methods. Constraints in SkyBlue can be between arbitrary data (not just numbers), and a constraint may have multiple methods that allow it to be satisfied in multiple directions. When variables are changed, local propagation is used to quickly re-satisfy the constraints. SkyBlue incrementally re-satisfies the set of constraints as new constraints are added and existing constraints are removed.
SkyBlue uses strengths associated with constraints (constraint hierarchies) to control which solution to choose if all constraints cannot be satisfied, or if there is more that one possible solution.
SkyBlue is presented in [SkyBlue] along with a pseudo-code implementation of the basic SkyBlue constraint solver. SkyBlue seemed to be the best possible (efficient) constraint solver, and we therefore decided to base the BETA constraint system on the SkyBlue algorithm.
The first step was now to realize the basic SkyBlue constraint solver in BETA. Based on the pseudo-code in [SkyBlue], it was surprisingly easy to write the appropriate BETA implementation.
Based on this basic SkyBlue constraint solver in BETA, we began the design and realization of a framework for constraints in BETA (described in more detail in the following sections). The design is intended primarily to create a basic framework to be specialized towards specific application domains. This basic framework is used in the design and realization of a constraint system for graphical layout.
The system should define suitable classes for constraints allowing dynamic assertion of constraint in a BETA program, just as other classes are used.
Since different application areas requires different kinds of constraints, the system should allow the user to develop specialised classes to meet specific requirements.
Recently constraint imperative languages like Kaleidoscope have become available for using constraints in application areas where imperative programming languages have been common, e.g. interactive graphical user interfaces. Intuitively the declarative style of constraints and the imperative style of assignments are conflicting. What should happen if a variable, say i, is constrained to be equal to 87 and the destructive assignment i:=117 is executed? Should the assignment fail (violating the semantics of the imperative language) or should the constraint be broken (violating the semantics of the constraint language)?
These conflicting issues may seem to make a reasonable mixed-paradigm language impossible. On the other hand there are situations where the ability of the system to maintain relations is very attracting, and where the possible conflicts of destructive assignment and declarative statements can be dealt with in a consistent way. This includes maintaining positioning of inter-related objects in a graphics display, where the possibility of stating the relations declaratively saves hundreds of lines of code that would have to be written in order to maintain the relations in response to user interaction.
In BETA, this may be compared to the runtime overhead due to the automatic garbage collection performed by the runtime system.
It may be the case that the runtime overhead due to constraints is acceptable, but this has to be investigated by using constraints in real-world applications. On the other hand, using constraints in BETA may also lead to new ways of solving problems or even give rise to new program designs.
Integrating constraints in the language has thus benefits, but it can also impose restrictions, especially when a program written in the language does not use constraints. If the underlying system has a built-in runtime overhead because of the constraints, its performance may suffer too much when constraints are not used. This is not desirable because it restricts the mixed paradigm languages from being a true union of its components: Its imperative part becomes inefficient even when its constraint part is not used.
Another solution is to model constraints in the imperative language. In BETA, this approach is used by developing general frameworks that can be tailored for special purposes, see [Nørgaard].
A general constraint framework may consist of an abstract constraint pattern defining abstract properties of constraints. The abstract constraints can then be specialised to model specialised constraints, e.g. for solving constraints pertaining to graphical representation of objects.
Because the constraints are modelled in BETA, this approach is properly inherently slower than the Kaleidoscope approach. Similarly, the task of defining constraints becomes slightly more complicated, because it is necessary to perform the compilation of user-defined complex constraints into simple constraints over integers by writing the code explicitly. On the other hand, the work has to be done only once and after the definition of the complex constraints, asserting these constraints is just as easy in the framework case as in case of a compiled constraint.
The framework approach has the advantage of being a true union of the object oriented language and the constraint language. This means that applications not using constraints are not affected by any runtime overhead from the constraint system.
Constraints can be viewed as "links" between objects defining relations maintained by the system. Such links should, once declared by the programmer, be maintained entirely by the system, thus freeing the programmer for other tasks without having to worry about the relations, i.e. the links created should be unbreakable (unless, of course, the programmer explicitly breaks it). The links should also be so "thin" that nobody notices them i.e. the overhead due to the underlying constraint solver should be negligible for reasonable applications compared to what could be accomplished by solving the actual problem without constraints.
The GLEIPNER framework defines the concept of a general constraint as two abstract classes, the Variable class and the Constraint class.
Variable:
(# ...
Class:< Object;
Value: @Class;
ValueChanged:<
(# v: ^Class
do GetValue->v[]; inner
#);
SetValue:<
(# v: ^Class
enter v[]
do inner; ...
#);
GetValue:<
(# v: @Class
do inner
exit v[]
#);
enter SetValue
exit GetValue
#);The
Variable class defines a virtual class, Class, that can be further
bound by the user to any subclass of the BETA Object class, that is any class
except char, boolean, integer and real. In the case that one of these classes
is needed the appropriate charObject, booleanObject, integerObject or
realObject must be used instead.In order to act as any other BETA object, instances of Variable class can be manipulated using traditional BETA message passing. To accomplish this, the Variable class defines two virtual procedure patterns, SetValue and GetValue. Since the general BETA object pattern at present contains neither an enter nor an exit part, the semantics of enter and exit parts of a Variable object must be specified in further bindings of SetValue and GetValue:
cInteger: Variable
(# Class::< IntegerObject;
SetValue::< (# do v->Value #);
GetValue::< (# do Value->v #);
#);cInteger
is an example of the definition of a constraint integer class.Although this might seem to be cumbersome to further bind these two virtuals in any user defined specializations of the Variable class, it turns out to be a very little extra work that has to be done, as in the above example. Moreover, these further bindings will always be the same as long as the (user defined) virtual Class has an enter and exit part.
Constraint:
(# Strength:< IntegerValue;
Method:
(# Inputs,
Outputs: @VariableList;
Init::< (# do ... #);
do inner;
#);
Add: (# do ... #);
Remove: (# do ... #);
Init::< (# do ... #);
do Init; inner;
#);The
Constraint class defines an abstract Method class that can be
used in specializations for stating how a given constraint should be satisfied.
Instances of Method contains two instance variables, Inputs
and Outputs that are used for storing references to the objects
controlled by that method; that is, the instances of class Variable,
constrained by this Constraint.A Constraint will be able to choose between several different instances of Class Method, thus implementing multi-directionality. The sets formed by Inputs and Outputs in a Method object must form a partition on the set of all variables constrained by this Constraint.
The current version of GLEIPNER will reject a method with non-disjoint Input and Output sets, and raise an exception. It is, however, the programmer's responsibility that the union of the Input and Output sets actually forms the set of all variables constrained by this Constraint.
Button: (# horizPos, vertPos: @Integer #); OK: @Button(# do OKaction #); Cancel: @Button(# do CancelAction #)In order to keep the two objects horizontally aligned one must be able to handle (at least) two different situations: OK is moved by user interaction and Cancel is moved by user interaction.
The horizontal and vertical relations are easily seen to be equal to maintaining the two constraints
OK.horizPos = Cancel.horizPos
OK.vertPos = Cancel.vertPos
This can be done easily in GLEIPNER by defining a constraint that captures the concept of equality:
Equal: Constraint
(# m1: @Method
(# Init::<
(#
do v1[]->inputs;
v2[]->Outputs;
#);
do v1->v2;
#);
m2: @Method
(# Init::<
(#
do v2[]->inputs;
v1[]->Outputs;
#);
do v2->v1;
#);
Init::<
(# do m1.Init; m2.Init #);
v1,v2: ^Variable;
enter (v1[],v2[])
do inner;
#);Note
that this definition of the equal constraint is entirely generic, and can be
imposed on all contraint variables. That is, the concept of equality
constraints can be defined in a library and reused in any constraint system.The various alignment relations can now be satisfied simply by creating an instance of Equal on the relevant objects:
(# Button:
(# horizPos,
vertPos:@IntegerObject
#);
OK: @Button(# ... #);
Cancel: @Button(# ... #);
do (OK.vertPos[],Cancel.vertPos[])
->Equal(# do Add #);
(* OK and Cancel are now
* horizontally aligned *)
#);GLEIPNER
supports hierarchical constraints, that is constraints with an associated
strength indicating how important it is for it to be satisfied. Once created by an execution of Init, a GLEIPNER Constraint object may be asserted by invoking the Add pattern. This will cause the constraint solver to try to satisfy the constraint, along with all other constraints that have been asserted.
GLEIPNER satisfies the constraints in such a way that a stronger constraint may never be left unenforced if it could be enforced by revoking another weaker constraint, i.e. the result of executing the methods in a Locally-Graph-Better method graph.
If the newly added constraint could not be satisfied because the system is overconstrained, a virtual NotEnforcedException is called by GLEIPNER. Normally NotEnforcedException will be further bound to display some kind of notification, since it may be confusing if the most recently added constraint is not satisfied immediately. Note however that NotEnforcedException should not always be considered an error, it simply indicates that a constraint could not be enforced right away.
Also, an added constraint that has been satisfied may be broken by GLEIPNER, if this allows stronger unsatisfied constraints to be satisfied by enforcing them and execute their methods.
If, for some reason, a constraint must be satisfied at all times, it should be declared as a required constraint. This does not always ensure that the constraint can be satisfied. It does, however, ensure that it will never be violated once enforced, since GLEIPNER never revokes a constraint that is not strictly weaker than some other unenforced constraint. A required constraint that is enforced thus remains "sacred" until it is revoked due to an explicit request from the programmer by invoking the Remove pattern.
The underlying implementation of GLEIPNER is built on top of the SkyBlue algorithm. Most of the code in the implementation of GLEIPNER is actually identical to the original SkyBlue, but some changes has been made.
The modifications can roughly be divided into two groups: Changes that was necessary because of the design of GLEIPNER, and changes pertaining to the fact that GLEIPNER itself is implemented in BETA. The first category contains the fundamental changes to the SkyBlue algorithm itself whereas the second one constraints changes made in the SkyBlue algorithm mainly to achieve better performance.
Another way of describing the difference between the two categories is that the former are changes pertaining to the modelling abstract constraints, which is, in principle, a language independent abstraction (of course we tacitly assumes that the language has class abstractions). The latter are changes pertaining to the primitives and abstractions available in the particular language.
Since a BETA object interacts with other objects using message passing and by evaluation of enter and exit parts, the SkyBlue requirement of variables being manipulated solely by constraints had to be abandoned.
Instead, a GLEIPNER variable has been modelled such that it can be manipulated directly. This demands a change in the underlying SkyBlue implementation in order to ensure that the system is perturbed, if necessary.
Similarly, some mechanism is provided for notifying the world outside the constraint solver that values have been changed due to value propagation. Specifically, a virtual ValueChanged is called when the value of a constrained variable have been changed.
The notion of enter and exit parts on the GLEIPNER variable class along with the virtual ValueChanged pattern makes the use of Input and Output constraints that are discussed in [SkyBlue] unnecessary.
An unfortunate effect on changing the semantics of direct value assignment to constrained variables is that the rules for invalidating propagation plans must be changed. In the current implementation this is handled by adding a temporary constraint (because this automatically guaranties that the method graph is locally-graph-better). Adding a constraint also triggers a value propagation, such that the assignment is done correctly and all affected variables are updated accordingly. Finally, the temporary constraint is removed, yielding a new locally-graph-better method graph.
It is possible to extract a valid propagation plan when the temporary constraint has been added, and executing this propagation plan will result in a correct propagation from this variable and downstream. Unfortunately removing the temporary constraint afterwards immediately (and correctly!) invalidates the extracted propagation plan.
A careful redesign of SkyBlue is needed here, possibly involving redesign of the datatype of propagation plans etc. in order to improve performance when propagating values.
In one test program using an early version of GLEIPNER with a slightly different implementation, an improvement of roughly 20% was gained when introducing propagation plans.
Automatic memory management is, however not costless. and BETA programs that create lots of objects during execution suffer from bad performance, because the runtime system triggers lots of garbage collection cycles.
In the GLEIPNER implementation this strategy has been applied in three major areas.
* Avoiding recursion.
The depth-first search with backtracking in SkyBlue is implemented using three mutually recursive procedures. In GLEIPNER, this has been rewritten into three static objects and the local scope in the recursion is implemented using an explicit stack for local variables. Therefore a recursive call does not create new objects.
* Using dedicated datastructures.
GLEIPNER uses basically two datastructures, lists and stacks. The BETA environment offers a class library with both list and stack patterns, but since these patterns defines interfaces to internal structures (encapsulating private data) each operation on such an object allocates an object. To avoid this, GLEIPNER has defined its own list and stack patterns, where operations does not allocate objects.
The impact on performance when avoiding excessive generation of objects is remarkable. In one case the time for updating the graphics display went from more than 1 minutes down to 2-5 seconds.
By changing MacEnv slightly (i.e. introducing a few patterns in the Window class) and by using specialised GLEIPNERs, it is possible to obtain tailorability.
The WindowItem class has been extended with four instances of class cInteger: cLeft, cTop, cRight and cBottom. Each of these objects are a wrapper of a corresponding MacEnv pattern, e.g. cLeft corresponds to the Left attribute of the WindowItem class. The virtual ValueChanged of each of the objects has been further bound to update its corresponding MacEnv pattern.
The changes in MacEnv are shown below omitting details.
Window: InterfaceObject
(# ConstraintSystem:< Gleipner;
cs: @ConstraintSystem;
WindowItem: InterfaceObject
(# cLeftDesc:< cs.cInteger
(# ValueChanged::<
(# do inner #);
#);
cLeft: @cLeftDesc;
...
cTop: @cTopDesc;
cRight: @cRightDesc;
cBottom: @cBottomDesc;
...
#);
...
#);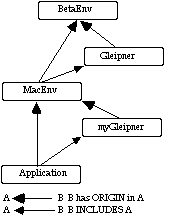
The fragment myGleipner has origin in MacEnv and is declared as a WindowLib. It is then allowed to refer to any name visible from the class Window. Since the Gleipner fragment is included from the MacEnv fragment, it becomes visible from the myGleipner fragment as well. Now a subclass of class Gleipner with constraint classes using MacEnv classes can be defined in the myGleipner fragment.
Finally, an application with origin in MacEnv and including myGleipner may further bind the virtual ConstraintSystem pattern of the MacEnv Window to myGleipner. It then becomes possible to use constraints on any object that are instances of classes declared inside the Window class.
We also show that constraints may be used to realize a generalisation of the Canvas class. A Canvas is the only WindowItem in MacEnv that is capable of containing other instances of WindowItem.
(# cs: @ConstraintSystem
(# cInteger: Variable
(# vClass::<
IntegerObject;
SetValue::<
(#
do v->Value;
inner
#);
GetValue::<
(#
do Value->v;
inner
#);
#);
Conversion: @Constraint
(# C2F: @Method
(#
do 32+((c*9)div 5)->f
#);
F2C: @Method
(#
do ((f-32)*5)div 9->c
#);
c,f: ^cInteger;
enter (c[],f[])
do Add;
#);
#);
Centigrade,
Fahrenheit: @cs.cInteger;
do (Centigrade[],Fahrenheit[])
->cs.Conversion;
100->Centigrade;
(* 100deg.C = 212deg.F *)
32->Fahrenheit;
(* 0deg.C = 32deg.F *)
#)The result is a hierarchy of nesting coordinate systems and a number of objects being displayed using only relative coordinates in one of the coordinate systems in the window.
This kind of clustering is done in MacEnv by means of inserting a Canvas object for each local coordinate system. There are, however, problems with this approach.
Firstly a Canvas is itself an object with a bounding frame. Hence it must be large enough to contain all its children. If the children are to be allowed to move around arbitrarily the only way is to make the size of the Canvas equal to the window. This means in turns that the position of the Canvas becomes equal to (0,0) in global window coordinates, thus destroying the notion of a local coordinate system.
Secondly, even in cases where it is possible to restrict the positions of the child objects of a Canvas, problems arises if different Canvases overlap. This pertains to the event handling inside the window, where events are dispatched to the front object in case that objects overlap. For this reason all objects belonging to all canvases layered under other canvases are virtually disabled, i.e. they will never receive any events.
It should be evident that for these reasons the Canvas abstraction is ill-suited for implementing such relations as positions of objects in local coordinate systems.
On the other hand the idea of grouping objects by an offset relative to a local coordinate system fits elegantly into the constraint programming paradigm.
By using Plus constraints appropriately it is possible to model the exact mathematical relation between objects belonging to the same coordinate system. It is even possible to specify a hierarchy of local coordinate systems where the origin of one system may be changed due to actions performed on objects belonging to another system.
The following simple application shows how to manipulate groups of objects
belonging to different coordinate systems. The example shows a tree, where each
subtree forms a local coordinate system. Every time an object is moved by user
interaction, a local coordinate system is translated causing all of its objects
to move.
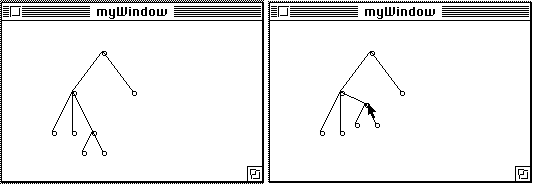
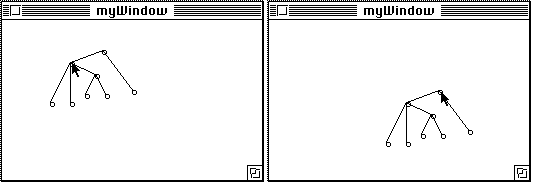
Bearing in mind that the problem is very difficult to solve using the ordinary MacEnv Canvases, the source code for the program is surprisingly simple. The constraint that is used, i.e. the Tree constraint, a subclass of the LocalSystem constraint takes a list of WindowItems along with the single WindowItem that is the root of the tree, i.e. origin in the local coordinate system. The last integer parameter indicates the level of the new coordinate system with respect to other systems.
TreeWindow: @Window
(# ...
(* create the nodes in the tree *)
o1: @Oval (# ... #);
o2: @Oval (# ... #);
o3: @Oval (# ... #);
o4: @Oval (# ... #);
o5: @Oval (# ... #);
o6: @Oval (# ... #);
o7: @Oval (# ... #);
o8: @Oval (# ... #);
Open::<
(# l1,l2,l3: @WIList;
do ...
(* initialize input lists *)
o2[]->l1.append;
o3[]->l1.append;
o4[]->l2.append;
o5[]->l2.append;
o6[]->l2.append;
o7[]->l3.append;
o8[]->l3.append;
(* create a tree *)
(1,o1[],l1[])
->cs.tree;
(* create a subtree *)
(3,o2[],l2[])
->cs.tree;
(* create another subtree *)
(5,o6[],l3[])
->cs.tree;
#);
#);The
implementation of the Tree and LocalSystem constraint may be found in
the appendix (but really, they are simple, too).The notion of the generalised Canvas in terms of local coordinate systems is in the authors opinion one of the most interesting new ideas that have evolved from the GLEIPNER framework so far. An obvious application area of generalised canvases is for implementing various browsers, e.g. fragment browsers like in Freja and ApplBuilder see [Møller] and [Grønbæk].
It is certainly true that constraints offer more powerful abstractions than what is available in a traditional object oriented programming language. The declarative style of constraint programming sometimes yields more beautiful programs, but this is, of course, a matter of personal preference.
The question of whether or not the induced overhead due to the constraint solver is acceptable will only be answered by using GLEIPNER in larger applications.
Implementing this new algorithm should be done as soon as possible, because these two improvements are very important in order to make the constraint system even more interactive.
Also, the problem with extracting propagation plans conflicting with the adopted semantics of assigning to constrained variables must be solved.
Since we lack understanding of the nature of constraint programming, debugging facilities should be provided. One possible step in this direction might be to design some kind of visualisation tool for aiding in finding out which constraints are responsible for the current state in the program.
It has been showed in previous sections that constraints may be added in a highly interactive way using menus etc. One obstacle is that the constraints must have been defined beforehand, e.g. by writing a specialised constraint framework.
Integrating the BETA interpreter [Malhotra] with GLEIPNER could support defining new types of constraints on the fly, providing an even higher degree of interaction than offered already.
Although the current implementation of GLEIPNER has been optimised in many ways, higher efficiency could still be achieved.
Due to the design of the GLEIPNER classes the SkyBlue algorithm had to be modified slightly. At present one of the modifications excludes one of SkyBlue's optimisation techniques, i.e. using propagation plans.
A specialised GLEIPNER for use in graphics applications was presented. We showed that a number of interesting problems can be solved in a very elegant way using the notion of constraints. In particular the concept of generalised canvases was explained.
The current status of GLEIPNER is that it has become reasonably stable. In order to gain more experience in constraint programming it is necessary to involve more users.
Some constraints that cannot be solved by the current version of SkyBlue can be solved if the newest SkyBlue version is implemented in GLEIPNER. This should be done as soon as possible.
Finally a number of suggestions to further works on constraint programming using GLEIPNER was given.
[Grønbæk] Kaj Grønbæk, Anette Hviid, Randall H. Trigg, ApplBuilder - an Object-Oriented Aplication Generator Supporting Rapid Prototyping, DAIMI PB-366, Computer Science Department, Aarhus University, October 1991.
[Jaffar92] Jaffar, J., Michaylov, S., Stuckey, P. J. and Yap, R. H. C., The CLP([[Rfraktur]]) Language and System, ACM Transactions on Programming Languages and Systems, 14(3), p. 339-395, 1992.
[Lopez] Gus Lopez, Bjorn N. Freeman-Benson and Alan Borning, Kaleidoscope: A Constraint Imperative Programming Language, NATO Advanced Study Institute on Constraint Programming, Pärnu, Estonia, August 1993.
[Møller] Kim Jensen Møller, DesignEnv, Object-Oriented Environments - the Mjølner Approach, Prentice Hall, chapter 17, p. 248, 1993.
[Nørgaard] Claus Nørgaard and Elmer Sandvad, Reusability and Tailorability in the Mjølner BETA System, DAIMI PB-300, Computer Science Department, Aarhus University, January 1990.
[SkyBlue] Michael Sanella. The SkyBlue Constraint Solver. Technical Report 92-07-02, Department of Computer Science and Engineering, University of Washington, February 1993.
Stay: Constraint
(* Use this constraint to
* specify how easy the
* variable can be changed.
* This can be used for
* controlling the direction of
* value propagation in the
* constraint graph.
*)
(# m: @Method
(# Init::<
(# do v[]->Outputs #)
#);
Init::< (# do m.Init; #);
v: ^Variable;
enter v[]
do inner;
#);
Plus: Constraint
(* Maintains plus relation on
* integers, i.e. A + B = C
*)
(# m1: @Method
(# Init::<
(#
do add1[]->Inputs;
add2[]->Inputs;
sum[]->Outputs;
#);
i,j: ^IntegerObject;
res: @IntegerObject;
do add1->i[]; add2->j[];
i+j->res; res[]->sum;
#);
m2: @Method
(# Init::<
(#
do add1[]->Inputs;
sum[]->Inputs;
add2[]->Outputs;
#);
i,j: ^IntegerObject;
res: @IntegerObject;
do add1->i[]; sum->j[];
j-i->res; res[]->add2;
#);
m3: @Method
(# Init::<
(#
do add2[]->Inputs;
sum[]->Inputs;
add1[]->Outputs;
#);
i,j: ^IntegerObject;
res: @IntegerObject;
do add2->i[]; sum->j[];
j-i->res; res[]->add1;
#);
Init::<
(#
do m1.Init; m2.Init; m3.Init
#);
add1,add2,sum: ^cInteger;
enter (add1[],add2[],sum[])
do inner;
#);
Times: Constraint
(* Maintains times relation on
* integers, i.e. A * B = C
*)
(# m1: @Method
(# Init::<
(#
do mul1[]->Inputs;
mul2[]->Inputs;
prod[]->Outputs;
#);
i,j: ^IntegerObject;
res: @IntegerObject;
do mul1->i[]; mul2->j[];
i*j->res; res[]->prod;
#);
m2: @Method
(# Init::<
(#
do mul1[]->Inputs;
prod[]->Inputs;
mul2[]->Outputs;
#);
i,j: ^IntegerObject;
res: @IntegerObject;
do mul1->i[]; prod->j[];
j div i->res; res[]->mul2;
#);
m3: @Method
(# Init::<
(#
do mul2[]->Inputs;
prod[]->Inputs;
mul1[]->Outputs;
#);
i,j: ^IntegerObject;
res: @IntegerObject;
do mul2->i[]; prod->j[];
j div i->res; res[]->mul1;
#);
Init::<
(#
do m1.Init; m2.Init; m3.Init
#);
mul1,mul2,prod: ^cInteger;
enter (mul1[],mul2[],prod[])
do inner;
#);
LocalSystem: Constraint
(* Maintains a local coordinate
* system relation between the
* root and the WIs in the
* WIList.
*)
(# Init::<
(# curWI: ^WindowItem;
do root.cLeft[]
->stay(# strength::<
(# do str->value #)
do add #);
root.cTop[]
->stay(# strength::<
(# do str->value #)
do add #);
l.scan
(# ch,cv: ^cInteger;
p: @point;
h,v:
@integerobject;
do c.position->p;
root.position
->p.subtract;
p->(h,v);
&cInteger[]->ch[];
h[]->ch.init;
&cInteger[]->cv[];
v[]->cv.init;
ch[] ->stay(#
strength::<
(#
do str+1->value
#)
do add #);
cv[]->stay(#
strength::<
(#
do str+1->value
#)
do add #);
(root.cleft[], ch[],
c.cleft[])
->plus(# do add #);
(root.ctop[], cv[],
c.ctop[])
->plus(# do add #);
c[]->curWI[];
inner init;
#);
#);
str: @Integer;
root: ^WindowItem;
l: ^WIList;
enter (str,root[],l[])
do inner;
#);
Tree: LocalSystem
(* Maintains a local coordinate
* system relation between the
* root and the WIs in the
* WIList. Each leaf is
* connected to the root by a
* line.
*)
(# Init::<
(# ConnectLine: Line
(# cStarth: @cInteger
(# ValueChanged::<
(# p: @point;
do Start->p;
v->p.h;
p->Start;
#);
#);
cStartv: @cInteger
(# ValueChanged::<
(# p: @point;
do Start->p;
v->p.v;
p->Start;
#);
#);
cEndh: @cInteger
(# ValueChanged::<
(# p: @point;
do end->p;
v->p.h;
p->end;
#);
#);
cEndv: @cInteger
(# ValueChanged::<
(# p: @point;
do end->p;
v->p.v;
p->end;
#);
#);
Open::<
(#
do cStarth.init;
cStartv.init;
cEndh.init;
cEndv.init;
disable;
#);
#);
cl: ^ConnectLine;
do &ConnectLine[]->cl[];
cl.open;
(root.cleft[],cl.cStarth[])
->equal (# do add #);
(root.ctop[],cl.cStartv[])
->equal (# do add #);
(curWI.cleft[],cl.cEndh[])
->equal (# do add #);
(curWI.ctop[],cl.cEndv[])
->equal (# do add #);
#);
do inner;
#);
[2] In some object-oriented terminologies, this is also referred to as the aggregation hierarchy.
[3] It should be noted that the examples given in this paper is not complete examples. We have also eliminated minor annoying details of the current implementation to ease the presentation slightly.
[4] GLEIPNER is the name of the magic chain that is used to tie Fenrisulven. The chain is made out of the roots of mountains, the sound of the feets of the cat, the spoors of the bear, the breath of the fish, the beard of women and the saliva of birds The chain is thinner than any string, but stronger than any other chain.